多项目组合管理一般包含以下几个步骤:分类Categorize、风险分析Risk Analysis、评估Evaluate、优化Optimize、优先级排序Prioritize、管理Manage。

图1 项目组合管理
本文通过实例,介绍如何利用Excel建立数学模型进行“优化Optimize”阶段的工作。
1. “优化”阶段面临的问题
进入“优化”阶段,企业决策层需根据自身的资源(人员、资金、设备、空间)瓶颈,综合考虑其他决策要素,对项目进行取舍决策,即:选择最优项目组合,取得最大收益。
案例:

表1
如上表1所示,决策者面对10个项目(商业计划BP),10个计划累计需要:
.68个测试员;
.60个开发人员;
.资金2555 M(1M = 1百万)。
但企业实际拥有:
.45个测试员;
.40个开发员;
.资金1500M。
企业短期内无法扩充这些资源,因此,决策者需对这10个项目作出取舍,即:选择最优项目组合。
2. 案例分析
2.1目标
选择最优组合、取得最大ENPV(预计净现值Estimated Net Present Value)。
2.2受限资源
.测试员人数(45)
.开发员人数(40)
.投入资金总数(1500 M)
2.3 传统做法
按项目ENPV 从大到小进行排序,优先选择ENPV较大项目,结果如表2所示:选择项目组合5、4、10、1,项目组合总计ENPV 为3195 M,使用资金1475M、测试员32人、开发员28人。
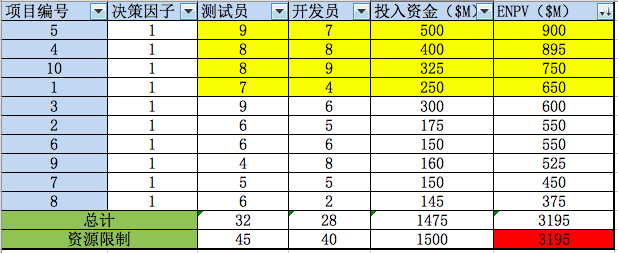
表2 传统ENPV排序做法
3. 数学建模实现项目组合管理“优化”
利用Excel 数学建模进行优化。Excel安装准备:使用Excel 规划求解Solver工具,请在“加载宏”内安装规划求解Solver组件。
3.1问题目标
资源受限情况下,实现项目组合总ENPV最大。
3.2 限制条件同2.2
3.3 操作步骤
步骤1:表格预处理
(1)引入“决策因子”。决策因子:
1:该项目被选中;
0:该项目未被选中。
(2)IF语句处理表格
使用IF 语句,处理表格1中“测试员”、“开发员”、“投入资金”、“ENPV”所有数据:
IF语句举例:
IF语句:IF(B2;项目优化!C2;0)
B2: 项目对应决策因子
C2:测试员数目
步骤2:打开Excel 规划求解工具
“数据”->“规划求解”
步骤3:设置目标:F12最大值
F12:SUM(F2:F11),所选项目组合的ENPV之和,如下图2所示。
图2 设置目标
步骤4:设置“可变参数”

图3 设置可变参数
B2:B11 10个“决策因子”设置为可变参数,图3所示。
步骤5:添加约束条件
(1)项目组合所需测试员总数 <= 45
图4 添加“测试员人数”约束
C12 <= C13
(2)项目组合所需开发员总数 <=40
图5 添加“开发员人数”约束
D12 <= D13
(3)项目组合投入资金总数 <= 1500 M
图6 添加“项目投入资金”约束
E12 <= E13
(4)决策因子“2进制”设置(决策因子只有0,1两个值)
图7 “决策因子”格式设置
B2:B11 格式设置为“二进制”;
选择“求解方法”为“演化”。
设置完毕后的“规划求解”操作界面:
图8 设置完成后的“规划求解”界面
步骤6:运行求解
运行“求解”后的界面如表3所示:
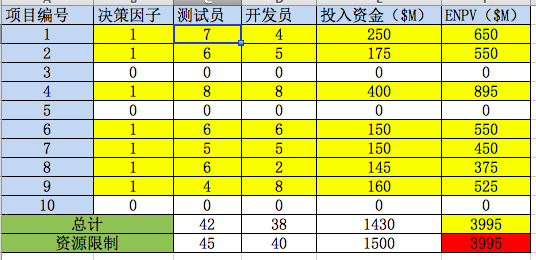
表 3
3.4结果分析
.优化后的项目组合:项目1、2、4、6、7、8、9;
.总ENPV:3995 M
对比利用传统ENPV排序法(总ENPV: 3195 M);
优化后,相同资源受限情况下,新的项目组合可为企业多创造800 M的收益。
后续思考:
1. 考虑企业长远利益,项目10必须入选最后项目组合,优化后的项目组合应该是?
2. 因项目关联性,项目2和项目3需同时入选,或同时落选,优化后的项目组合应该是?
3. 考虑项目相近性,项目1和项目2只能有且必须只有一个入选,优化后的项目组合应该是?